
By knowing the base area, one can calculate the volume.

Volume of Different Types of Oblique Prismsĭifferent types of prisms have different bases and hence have different base areas. This is because both have the same perpendicular height. The SI unit of volume is cubic meters.Īn oblique prism’s volume is equal to the volume of a right prism if both have the same bases. Where h is the height and B is the Area of the base of the prism. The formula for a prism’s volume is as follows: The volume is the space occupied by a solid object.
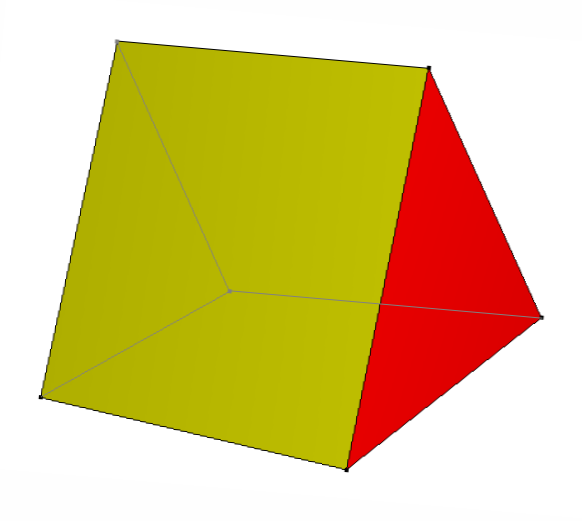
It is not common practice to calculate the surface area of an oblique prism as there is no direct formula. The surface area of an oblique prism is not easy to calculate. The faces or sides of the oblique prism are parallelograms which is a four-sided polygon with parallel opposite sides.įigure 2 shows a hexagonal oblique prism with a demonstration of its bases and lateral faces.įigure 3 – Illustration of Length, Base Area and Base Perimeter of a Rectangular Prism for Surface Area Lateral FacesĪ prism’s lateral faces are the faces that are on its sides instead of its top and bottom. These bases are parallel to each other regardless the prism is right or oblique.įor example, a pentagonal prism has two pentagons as bases on each end of the prism. The two bases are the two unique sides of a prism which defines the type of prism according to its shape. The edges of a prism are parallel to each other, extending from one base to the other. It has equal cross-sections with identical bases. It is a polyhedron with flat faces, straight edges, and sharp vertices. To understand an oblique prism comprehensively, first, we need to know about the “ prism.” PrismĪ three-dimensional object with two same ends is known as a prism. 544 square units.Figure 1 – An Oblique Prism with Height h So the surface area of this figure is 544.
#Square triangular prism plus#
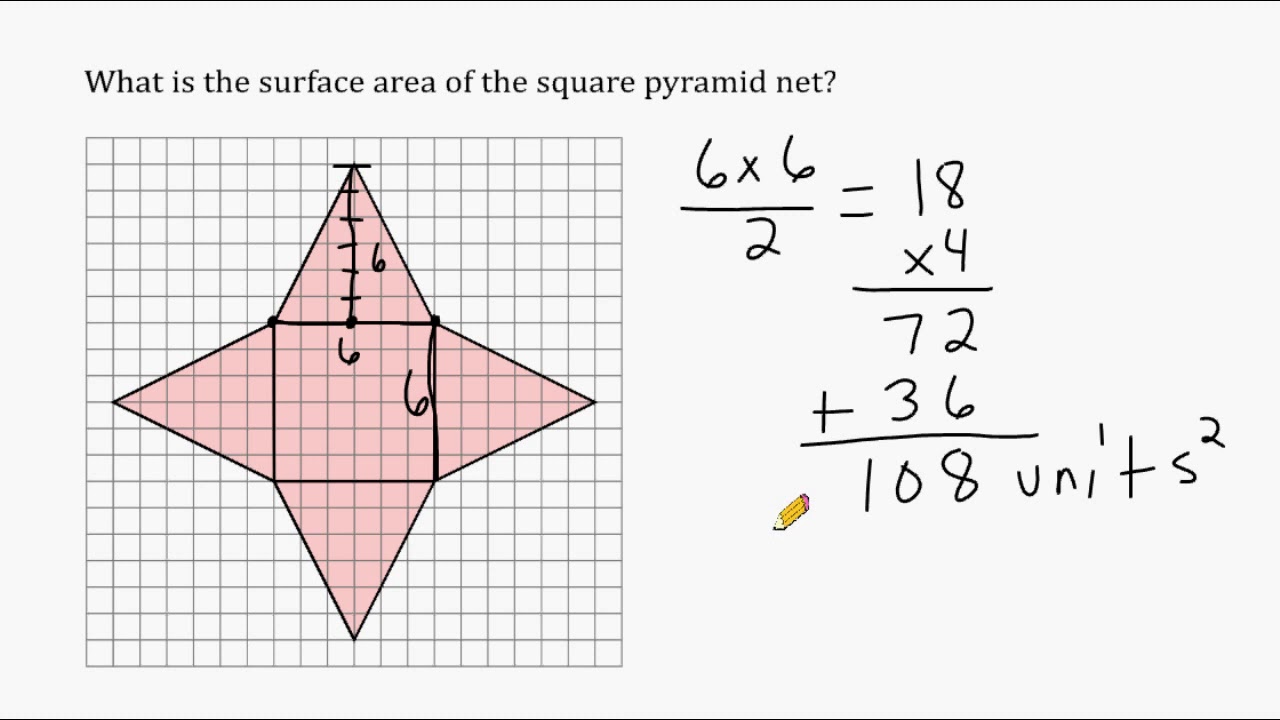
So one plus nine is ten, plus eight is 18, plus six is 24, and then you have two plus two plus one is five. To open it up into this net because we can make sure We get the surface area for the entire figure. And then you have thisīase that comes in at 168. You can say, side panels, 140 plus 140, that's 280. 12 times 12 is 144 plus another 24, so it's 168. Region right over here, which is this area, which is Just have to figure out the area of I guess you can say the base of the figure, so this whole And so the area of each of these 14 times 10, they are 140 square units. Now we can think about the areas of I guess you can consider It would be this backside right over here, but You can't see it in this figure, but if it was transparent, if it was transparent, So that's going to be 48 square units, and up here is the exact same thing. Thing as six times eight, which is equal to 48 whatever Here is going to be one half times the base, so times 12, times the height, times eight. Of this, right over here? Well in the net, thatĬorresponds to this area, it's a triangle, it has a base So what's first of all the surface area, what's the surface area We can just figure out the surface area of each of these regions. So the surface area of this figure, when we open that up, And when you open it up, it's much easier to figure out the surface area. So if you were to open it up, it would open up into something like this. Where I'm drawing this red, and also right over hereĪnd right over there, and right over there and also in the back where you can't see just now, it would open up into something like this. It was made out of cardboard, and if you were to cut it, if you were to cut it right Video is get some practice finding surface areas of figures by opening them up intoĪbout it is if you had a figure like this, and if


 0 kommentar(er)
0 kommentar(er)
